Улитка Паскаля (или Лимакон Паскаля)

Была открыта Этьеном Паскалем ( отцом Блеза Паскаля) и названа другим французом Gilles-Personne Roberval в 1650 году, когда он использовал ее как пример его методов проведения касательных, то есть дифференцирования. Ее название произошло от латинского limax, что значит - улитка. В 1625 Этьен Паскаль в своей переписке с Мерсенном, у которого частенько собирались за чашкой чая знаменитые геометры, в том числе и Gilles-Personne Roberval, описал метод построения новой кривой, обладающей интересными свойствами (которую впоследствии назвали Улиткой), и те посоветовали ему опубликовать свои изыскания в "Underweysung der Messungpublished", который пользовался их уважнием.

Трисекция угла с помощью улитки Паскаля

Задача о трисекции становится разрешимой в общем случае, если не ограничиваться в геометрических построениях только классическими инстрементами - линейкой и циркулем. Например, Гиппий Эпидский ( IVвек до нашей эры) для трисекции угла пользовался квадратриссой, александрийский математик Никомед (II век до нашей эры) использовал кривую, названную кривой Никомеда.

Опишем метод деления произвольного угла на три равные части с помощью кривой, названной улиткой Паскаля , в честь французского физика и математика Блеза Паскаля (1623 - 1662). Каждый читатель может легко построить эту кривую самостоятельно.

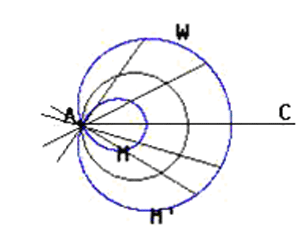
Для построения улитки Паскаля достаточно нарисовать окружность W произвольного радиуса R = a, выбрать на ней некоторую точку А и начать вращать вокруг точки А луч АС. Если по обе стороны от второй точки пересечения луча АС с окружностью на луче АС откладывать отрезки, равные радиусу исходной окружности ( R = a), то получится два набора точек - М и М’.
Улитка Паскаля - геометрическое место точек М и М’.
Для завершения построения через полученные точки достаточно провести плавную непрерывную линию.

Выполним трисекцию произвольного угла с помощью улитки Паскаля

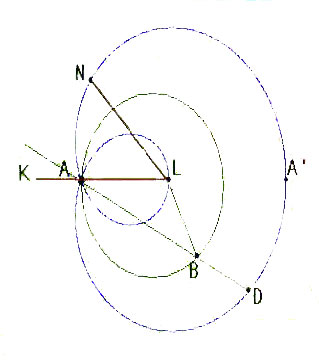
Пусть требуется разделить на три равные части данный угол KLN. Для этого вычерченная на кальке улитка Паскаля накладывается на угол KLN таким образом, чтобы центр образующей окружности совпал с вершиной угла, а ось улитки АА’ - совпала со стороной угла KLN. Точку Д (точку пересечения угла с улиткой) соединим с точкой А. Тогда угол AДL будет искомым, то есть угол AДL = 13 угла KLN.

Доказательство:
соединим точку В ( в которой образующая окружность пересекает АД ) с точкой С.
Треугольники ABL и LBД - равнобедренные, так как АL = LB = BД = а. Угол BDL = x следовательно, угол BLД = x , таким образом получаем, что угол ABL = 2x, следовательно, угол BAL = 2x.
Отсюда угол KLN = угол Д + угол BAL = x+2x.
Получаем : Х = 13 угла KLN.


« назад в меню