На продолжении ребра BB1 призмы ABCA1B1C1 взята точка B2, а в грани ACC1A1 - точка P. Постройте точки пересечения прямой B2P с плоскостями оснований призмы.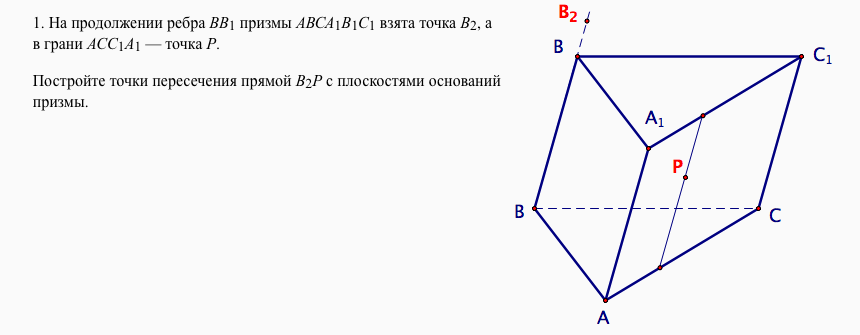

Сечение призмы плоскостью В2РQ. Параллельно АД через точку Р проводим прямую до рёбер. Получим на АА1 точку К, на ДД1 точку М. Соединим К и В2. Проведём линию через В2 и Q до пересечения с СС1 в точке Е. Соединим точку М с точкой Е. Искомое сечение В2КЕ.                      Точки пересечения прямой В2Р. Обозначим точку пересечения перпендикуляра на котором лежит точка Р с ребром А1С1  К, а с ребром АС  М.  Проведём В1К. Получим одну точку на пересечении линий В2Р и В1К. Проведём линию через точки В и М. За пределами призмы продолжение линий В2Р и ВМ дадут вторую точку.          Средний чертёж. Через точку Р параллельно АД проводим линию до пересечения с АА1 в точке К и ДД1 в точке М. Соединим В2 и К. Через М и Q проведём линию до пересечения с СС1 в точке Е. Тогда В2ЕМК след плоскости.