Определите площадь заштрихованной на рисунке фигуры, если О1 - центр окружности с радиусом 4 см, угол АО1В = 120º, О2 - центр окружности с диаметром АВ. (рисунок во вложенном файле) 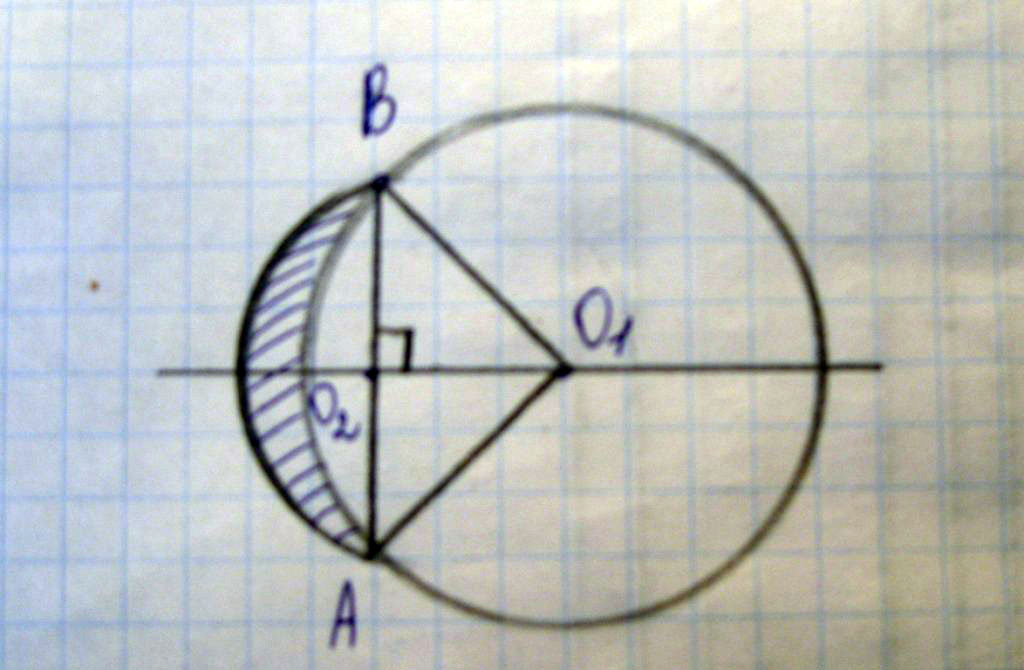
1) найдем площадь сектора малой окружности $$ S1=\frac{\pi*R^{2}}{2} $$ 2) Найдем площадь сектора большой окружности$$ S2=\frac{\pi*R^{2}}{3} $$3) Найдем площадь треугольника АО1ВАВ=2Rsin$$ 60^{0} $$ (половины угла AO1B) О1О2=Rcos$$ 60^{0} $$S3=AB*O1O2/2=$$ R^{2}sin(\frac{\pi}{3})cos(\frac{\pi}{3}) $$4) Найдем площадь, ограниченную АВ и большой окружностьюS4=S2-S35) Площадь искомой фигурыS=S1-S4=S1-(S2-S3)=S1-S2+S3
Похожие задачи:
1. В окружность радиуса 5 см вписан прямоугольный треугольник так, что один из его катетов вдвое ближе к центру, чем другой. Найти длину этих катетов. 2. В сектор АОВ с радиусом R и углом 90° вписана окружность, касающаяся отрезков ОА, 0В и дуги АВ. Найти радиус окружности. 3. В равнобедренной трапеции диагонали пересекаются под углом 60° Найти диагонали и нижнее основание трапеции, если верхнее основание 3 м, а боковая сторона трапеции 4 м. 4. Из точки N, лежащей вне окружности, проведены к ней две секущие, образующие угол 45°. Меньшая дуга окружности, заключенная между сторонами угла, равна 30°. Найти величину большей дуги. 5. Внутри параллелограмма взята произвольная точка, которую соединили со всеми его вершинами. Найти отношение суммы площадей двух противолежащих треугольников к сумме площадей. смотреть решение >> 