Докажите, что изображенные на рисунке треугольники подобны.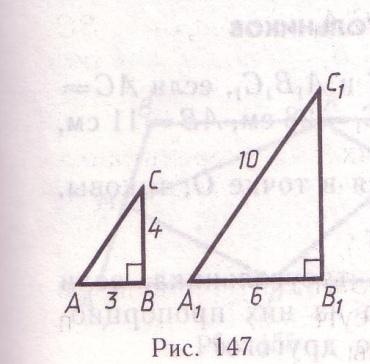

Подобие прямоугольных треугольников доказывается через равенство отношений двух сторон в данном случае возьмем гипотенузы AC и A1C1 и катеты AB и A1B1 должно выполняться равенство: AC/A1C1=AB/A1B1 известно всё кроме AC. Находим AC по теореме Пифагора:AC^2=3^2+4^2=9+16=25AC=5 Подставляем: 5/10=3/6
это верное равенство, значит треугольники подобны - доказано) 

на этом рисунке сразу видно что стороны АВ/А1В1=3/6=1/2.и углы С и С1 по 90 градусов. Найдем у второго треугольника сторону В1С1 по теореме Пифагора. В1С1^{2}=А1С1^{2}-А1В1^{2}=100-36=64. В1С1=8. тогда видно что сторона ВС/В1С1=4/8=1/2. из всего можно сделать вывод что треугольники подобны по двум сторонам и углу между ними.