1. Две окружности с центрами О и К имеют соответственно радиусы 4 и 8 см. Найдите радиусы окружностей, касающихся одновременно двух данных, если их центры лежат на прямой ОК, и отрезок ОК равен 6 см.

2. Высоты треугольника, пересекаясь в точке Н, образуют шесть углов с вершиной в точке Н. Определите эти углы, если углы данного треугольника равны: 50, 60, 70 градусов.

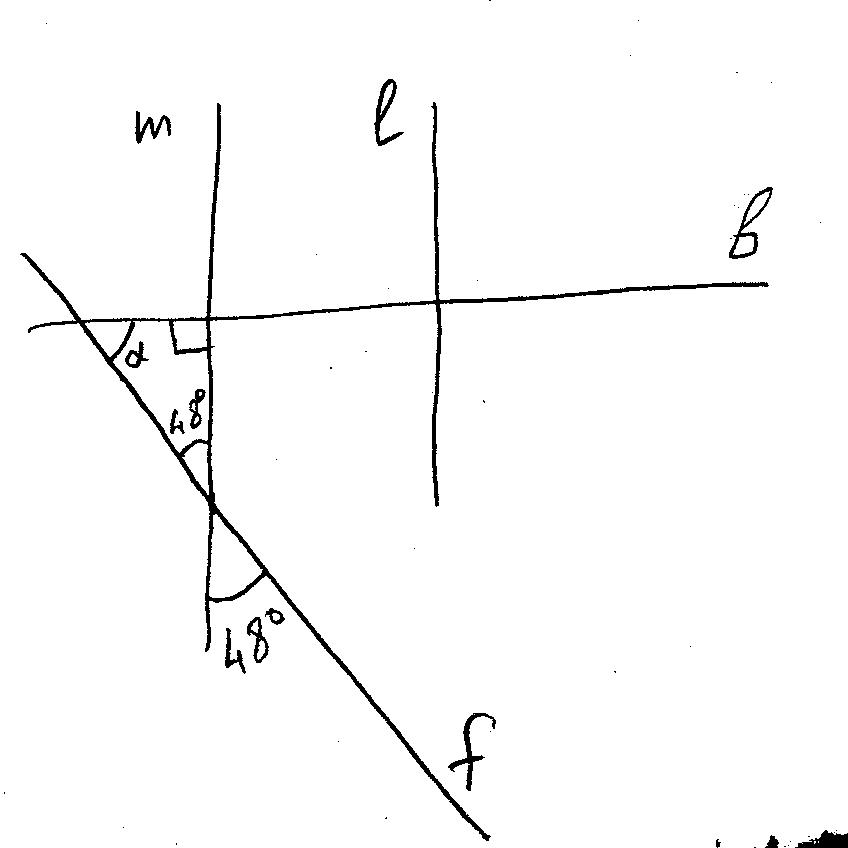
3. Прямые m и l параллельны, прямая b перпендикулярна прямой l, а прямая f пересекает прямую m под углом 48 градусов. Найдите угол между прямыми b и f

1)

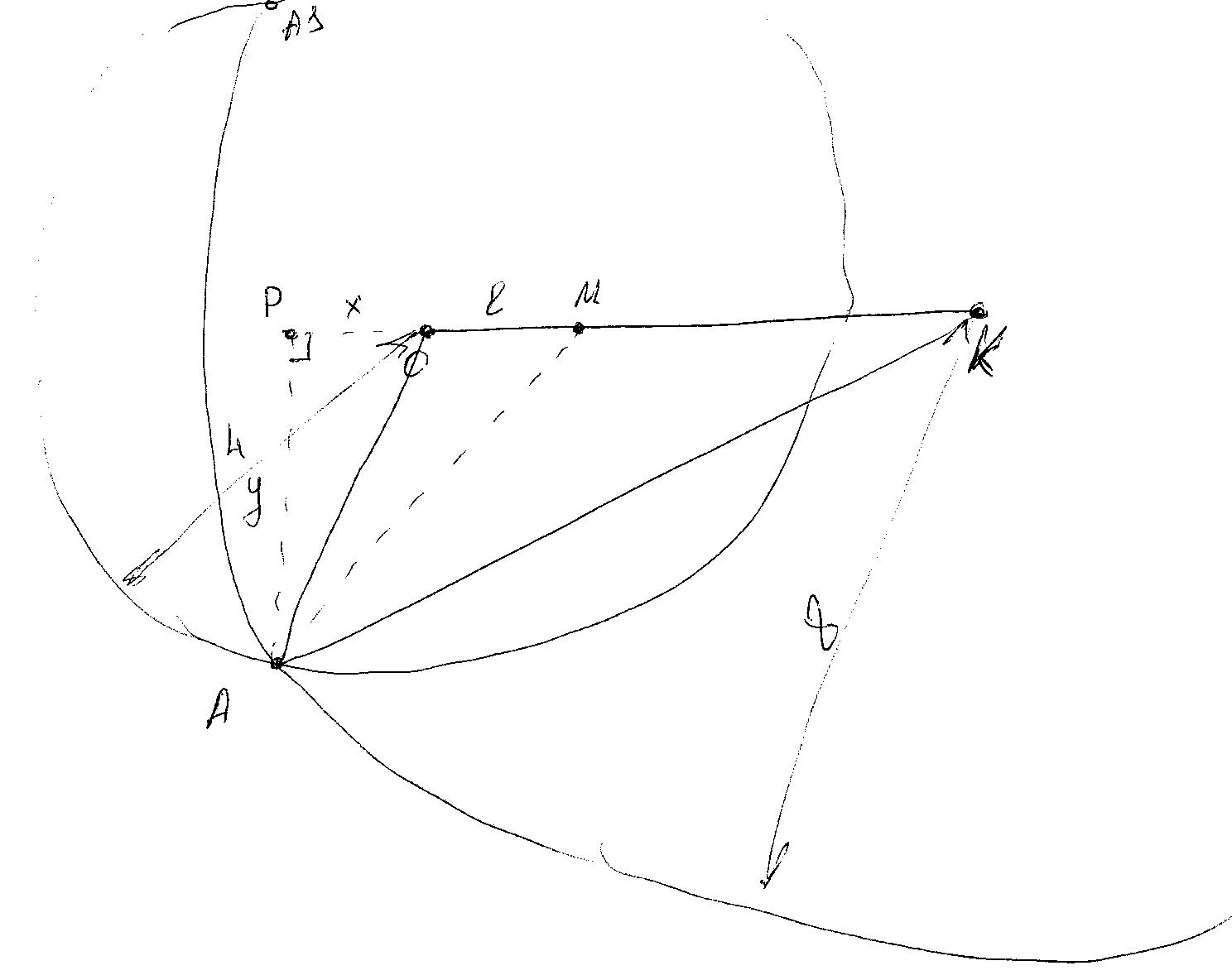
А и А1 точки пересечения окружностей с центрами О и К

АР перпендикуляр на продолжение ОК

АР=у

ОР=х

ОА=4

КА=8

ОК=6

х²+у²=4²=16

(х+6)²+у²=8²=64  ⇒ у²=64-(х+6)², подставляем в первое

х²+64-(х+6)²=16

х²+64-х²-12х-36-16=0

12х=12

х=1

у=√(16-1)=√15

l -расстояние от т. О до ц. окр. М касающихся одновременно двух данных, т.е. в т. А и А1 (необходимо найти МА)

МА²=(х+l)²+у²=(1+l)²+15

2)

АВС - треугольник, а=60, В=50, С=70, т. Н пересечение

АА1, ВВ1, СС1 высоты.

<АНС1=<СНА1=<3 (вертикальные)

ΔВНА1 подобен ΔВСВ1 ⇒

ΔВНС1 подобен ΔВАВ1 ⇒

ΔСНА1 полобен ΔСВС1 ⇒<СНА1=<В=50