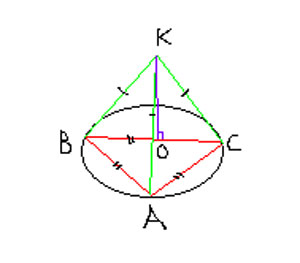
Площадь равностороннего треугольника равна 108√3 кв. см. (108 корень квадратный из 3). Точка К не принадлежит плоскости АВС. КА=КВ=КС=13 см. Найти расстояние от К до плоскости АВС.

площадь равностороннего треугольника:$$ S=\frac{a^2\sqrt{3}}{4} $$$$ 108\sqrt{3}=\frac{a^2\sqrt{3}}{4} $$$$ a=\sqrt{432} $$радиус описанной окружности:$$ R=OC=\frac{a\sqrt{3}}{3}=\frac{\sqrt{108}\sqrt{3}}{3}=12 $$$$ KO=\sqrt{13^2-12^2}=5 $$




Похожие задачи:
Шар касается сторон треугольника MKP, причем MK=4 см, MP=5 см, KP=7см. Центр шара- точка О находится от плоскости треугольника MKP на расстоянии, равном \( \frac{\sqrt{10}}{2}\). Найдите объем шара.


смотреть решение >>
Точка, лежащая в одной из пересекающихся плоскостей, удалена от второй плоскости на 6 см, а от линии их пересечения - на 12 см. Вычислите угол между плоскостями.

Даны точки М(3;0;-1), К(1;3;0), Р(4;-1;2). Найдите на оси Ох такую точку А, чтобы векторы МК и РА были перпендикулярны.

Две вершины равностороннего треугольника расположены в плоскости альфа. Угол между плоскостью альфа и плоскостью данного треугольника равен фи. Сторона треугольника равна m. Вычислите:

1) расстояние от третьей вершины треугольника до плоскости альфа;

2) площадь проекции треугольника на плоскость альфа.



смотреть решение >>
Треугольник ABC,площадь которого равна 24 см2, является ортогональной проекцией равностороннего треугольника A1B1C1 cо сторонами 8 см. Найдите угол между плоскостями ABC и A1B1C1
смотреть решение >>
Через точки B1 и B2 стороны AB равностороннего треугольника ABC проведены плоскости альфа и бета, параллельные прямой BC. 1) На какие фигуры делится этот треугольник плоскостями? 2) Вычислите периметры этих фигур, если AC=8 см и AB1=B1B2=B2B
смотреть решение >>
1. Через точки A и B, расположенные в перпендикулярных плоскостях, проведены к линии их пересечения перпендикуляры AC и BD. Вычислите длину отрезка CD, если AC=9см, BD=8см, AB=17см.


2. Через середину O катета MK прямоугольного треугольника MKP проведен к его плоскости перпендикуляр OI, равный \( a\sqrt{3} \), \( \angle K = 90° \), MK=4a, PK=b. Найдите: a) площади треугольника TPK и его проекции на плоскость треугольника MKP; b) расстояние между прямыми TO и PK.
смотреть решение >>