Дано: NM параллельно AC, AM=6см, BM=8см, AC=21 см. а) Доказать, что произведение Ab*Bn=CB*BM

б) найти MN

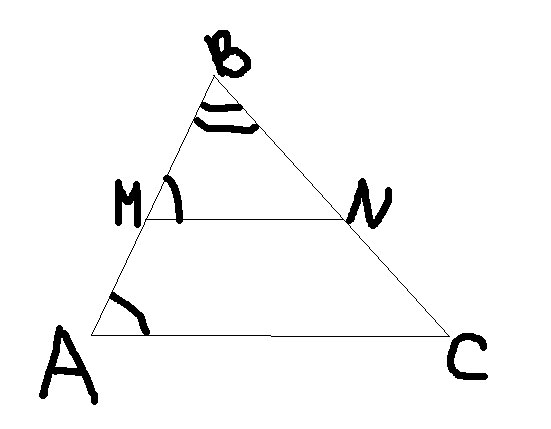
Рассмотрим треугольники АВС и BMN. Они подобны по первому признаку подобия: угол А равен углу М (соответственные углы при параллельных прямых), угол В - общий. Так как треугольники подобны, то ВМ/АВ=BN/BC, т.е. по свойству пропорции ВМ*ВС=BN*AB, ч.т.д.. Так как треугольники подобны, то MN/AC=BM/ABАВ=АМ+ВМ=6+8=14 смMN/21=8/14MN=8*21/14=12 (см) Ответ: MN=12 cм.