Определите площадь заштрихованной на рисунке фигуры, если О1 - центр окружности с радиусом 4 см, угол АО1В = 120º, О2 - центр окружности с диаметром АВ. (рисунок во вложенном файле)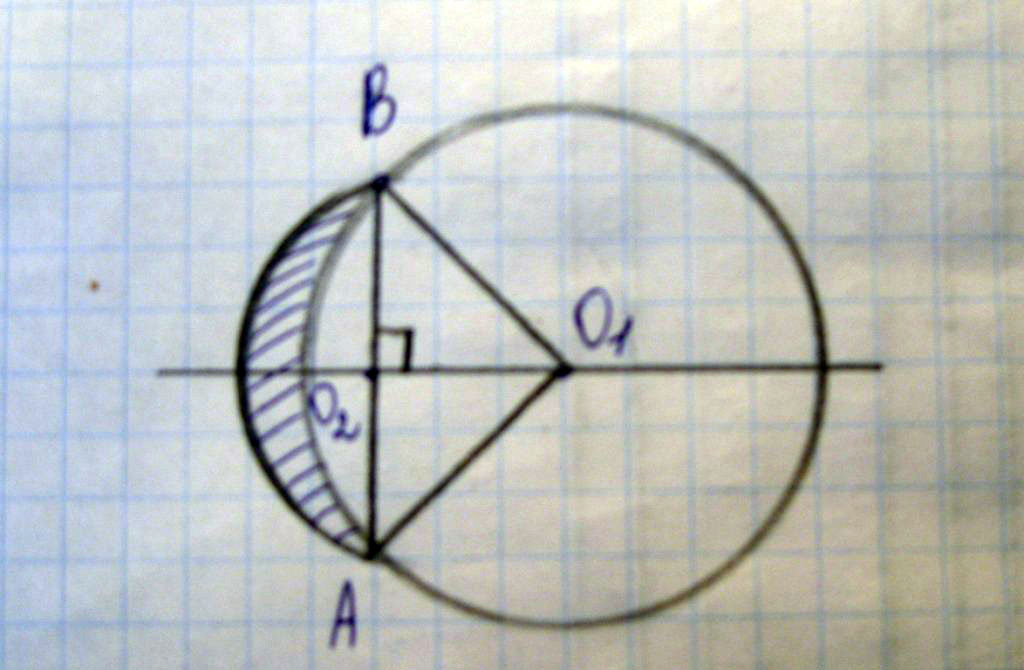

Для удобства обозначим на линии ОО1 точки её пересечения с окружностями. Первая по ходу от О2 будет М далее К. Центр малой окружности лежит на диаметре АВ(по условию). Значит слева от АВ имеем половину окружности с диаметром АВ(фигура АКВ) если из неё вычесть фигуру АМВ то получим площадь заштрихованной. фигуры. Найдём АВ как длину хорды. АВ=2Rsinа/2=2Rsin60=6,92. Площадь фигуры АКВ=половине площади круга=(пи Дквадрат/4):2=(пи АВквадрат)/8=18,8. Площадь фигуры АМВ найдём как площадь сегмента=Rквадрат/2*(пи *а /180-sinа)=Rквадрат/2(пи 120/180-sin 120)=9,76. (синус 120= синус60). Площадь защтрихованной фигуры=18,8-9,76=9,04.