В кубе ABCDA1B1C1D1 найдите угол между прямой AB1 и плоскостью ABC1.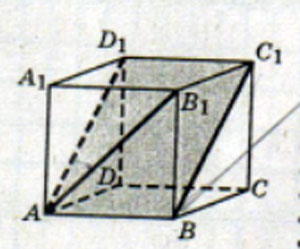

АВС1: векторы АВ1 и А1ДА(1;1;0) В1(1;0;1) АВ1{1-1;0-1;1-0}АВ1{0;-1;1}|AB1|=√0^2+(-1)^2+1^2=√2докажем, что ДА1 перпенд. АВС1:АВперп. АА1Д по свойству куба, значит АВперп. А1Д1 т.к. А1ДС(АА1Д)теперь, А1Дперп. АД1, т.к. диагонали квадрата взаимно перпендикулярны. А1Дперп. АД1 |  | => А1Дперп. АВС1 по призн. пер-сти прям.и плоск. знач. АД1перп. АВС1А1Дперп. АВ |АВ1*ДА1={0;-1;1}*{1;0;1}=0*1+(-1)*0+1*1=1sin(АВ1^(АВС1))=|cos(AB1^ДА1)|= |AB1*ДА1| / |AB1|*|ДА1|=1/√2*√2=1/2(AB1^(ABC1))=30 градусов. Ответ: 30 градусов.