В прямоугольном треугольнике ABC угол C прямой, угол B=72°. Найдите угол между высотой CH и медианой CM. Ответ дайте в градусах.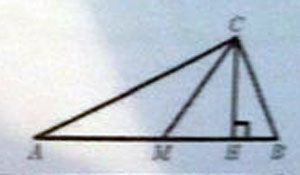

Медиана в прям. тр-ке всегда равна половине гипотенузы. СМ = СВЗначит тр-ик СМВ - равнобедренный и угол МСВ = углу В = 72 град. угол НСВ = 90 - 72 = 18 град (из тр-ка НСВ) Значит искомый угол МСН = МСВ - НСВ = 72 - 18 = 54 градОтвет: 54 град.

угол HCM=36 Т. К угол б=72, угол Н=(180-72-90)=18 т.к Н высота то она делит угол пополам следовательно угол НСМ=36