Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиус этой окружности, если: а) АС = 8см, ВС=6см; б) АС= =18 см, ∠B=30°.
Дано:
Решение:
Похожие задачи:
Подобны ли треугольники ABC и DEF, если ∠A= 106°, ∠B = 34°, ∠E = 106°, ∠F=40°, АС=4,4см, АВ = 5,2см, BC=7,6см, DE = 15,6см, DF=22,8см, EF=13,2см?
смотреть решение >>
смотреть решение >>
1. В равнобедренном треугольнике ABC с основанием AC проведена биссектриса AD. Найти углы этого треугольника, если угол ADB равен 110 град.
смотреть решение >>
2. В равнобедренном треугольнике DEK с основанием DK отрезок EF - биссектриса, DK = 16см, угол DEF равен 43 град. Найти углы DEK, EFD, KF.
3. В прямоугольном треугольнике ABC с прямым углом С, внешний угол при вершине A равен 120 град., AC+AB=18см. Найти AC и AB.
смотреть решение >>
1)через вершину С правельного трикутника АВС у якому АС= 8 см проведено перпендикуляр РС до площини трикутника. знайдіть кут між площинами АВС і АРВ якщо РВ =10 см. 2) дано трикутник АВС, площина альфа параллельна прямій АВ перетинає сторону АС в т. К ,а сторону ВС в т. М. знайдіть АВ якщо КС =12см АС = 18см КМ= 36см.
смотреть решение >>
смотреть решение >>
Дано: NM параллельно AC, AM=6см, BM=8см, AC=21 см. а) Доказать, что произведение Ab*Bn=CB*BM 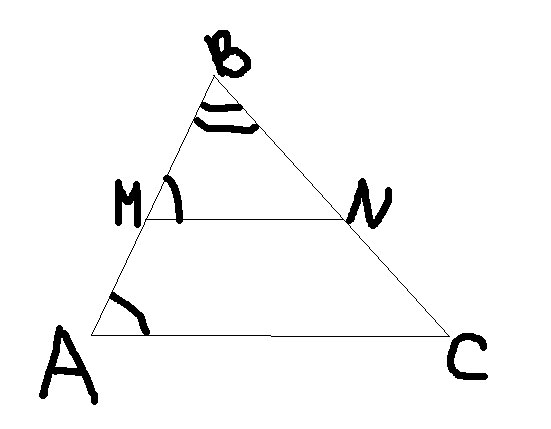
смотреть решение >>
б) найти MN
смотреть решение >>
1. Через точки A и B, расположенные в перпендикулярных плоскостях, проведены к линии их пересечения перпендикуляры AC и BD. Вычислите длину отрезка CD, если AC=9см, BD=8см, AB=17см.
2. Через середину O катета MK прямоугольного треугольника MKP проведен к его плоскости перпендикуляр OI, равный \( a\sqrt{3} \), \( \angle K = 90° \), MK=4a, PK=b. Найдите: a) площади треугольника TPK и его проекции на плоскость треугольника MKP; b) расстояние между прямыми TO и PK.
смотреть решение >>
2. Через середину O катета MK прямоугольного треугольника MKP проведен к его плоскости перпендикуляр OI, равный \( a\sqrt{3} \), \( \angle K = 90° \), MK=4a, PK=b. Найдите: a) площади треугольника TPK и его проекции на плоскость треугольника MKP; b) расстояние между прямыми TO и PK.
смотреть решение >>