Диаметр шара 25 см. На его поверхности даны точка А и окружность, все точки, которой удалены (по прямой) от А на 15 см. Найдите радиус этой окружности.
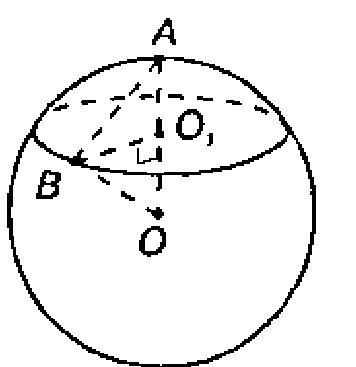
Радиус шара равен половине диаметра.
Так что
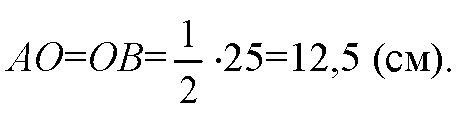
Далее, ΔАОВ равнобедренный (так как ОB=ОA) и АВ=15 см. Найдем площадь ΔАОВ по формуле:

Так что

Ответ: 12 см.
Похожие задачи:
1. В окружность радиуса 5 см вписан прямоугольный треугольник так, что один из его катетов вдвое ближе к центру, чем другой. Найти длину этих катетов. 2. В сектор АОВ с радиусом R и углом 90° вписана окружность, касающаяся отрезков ОА, 0В и дуги АВ. Найти радиус окружности. 3. В равнобедренной трапеции диагонали пересекаются под углом 60° Найти диагонали и нижнее основание трапеции, если верхнее основание 3 м, а боковая сторона трапеции 4 м. 4. Из точки N, лежащей вне окружности, проведены к ней две секущие, образующие угол 45°. Меньшая дуга окружности, заключенная между сторонами угла, равна 30°. Найти величину большей дуги. 5. Внутри параллелограмма взята произвольная точка, которую соединили со всеми его вершинами. Найти отношение суммы площадей двух противолежащих треугольников к сумме площадей. смотреть решение >>