Вiдрiзок CD - висота трикутника ACK, зображеного на рисунку, CK = 12см, DK=3√7 см. Знайдiть довжину вiдрiзка AD.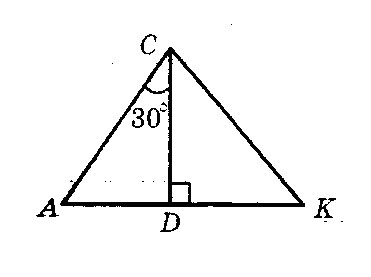

за теоремою піфагора

$$ CD^{2} = CK^{2} - DK^{2} $$

$$ CD^{2} = 12^{2} - (3sqrt{7})^{2} $$

 $$ CD^{2} = 144 - 63 = 81 $$

CD = 9

за теор. (катет що лежить навпроти кута 30 градус. дорівнюе половині гіпотенузи) 

AC = 2х; AD = х

за теор. Піфагора 

$$ CD^{2} = AC^{2} - AD^{2} $$

$$ 9^{2} = (2x)^{2} - x^{2} $$

$$ 81 = 4x^{2} - x^{2} $$ 

$$ 3x^{2} = 81 $$ 

$$ x^{2} = 27 $$ 

$$ x = 3sqrt{3} $$ (см) - (AD)

$$ AC = 3sqrt{3} x 2 = 6sqrt{3} (см) $$