Допустим, что дан треугольник АВС -
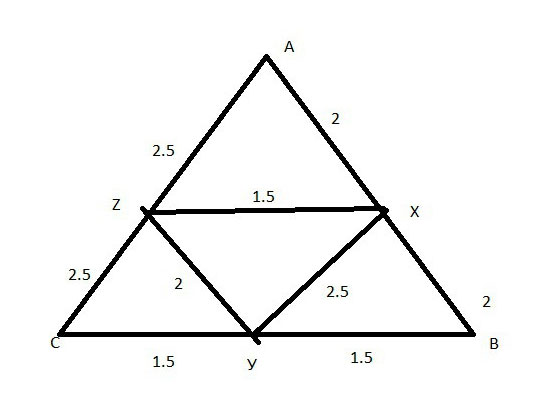
 СВ = 3 см - XZ-средняя линия
АВ = 4 см - УZ-средняя линия 
 СА = 5 см- XУ-средняя линия
Cредняя линия равна половине основания
XZ=СВ/2=3/2=1.5см
УZ= АВ/2=4/2=2см
XУ=СА/2= 5/2=2.5см
Средняя линия в точках пересечения со сторонам делит их пополам т.е:
СУ=УВ=СВ/2=1.5см
АХ=ХВ=АВ/2=2см
СZ=ZA=СА/2=2.5см
Как мы видим из вычислений и рисунка все 4 маленьких треугольника равны по трем сторонам (это третий признак равенства) 
Мы знаем  все стороны маленьких треугольников, значит, по формуле Герона мы можем найти площадь:
$$S= \sqrt{p(p-a)*(p-b)*(p-c)}$$
p- полупериметр, a,b,c- стороны
$$p= \frac{2+2.5+1.5}{2}$$
$$p= \frac{6}{2}$$
$$p=3$$
$$S= \sqrt{3(3-1.5)*(3-2)*(3-2.5)}$$
$$S= \sqrt{3*1.5*1*0.5}$$
$$S= \sqrt{2.25}$$
$$S= 1.5 cm^{2}$$
Мы нашли площадь одного маленького треугольника, а он в тетраэдре  является гранью. Т.к мы доказали, что маленькие треугольники равны, то площади граней тоже равны  

Похожие задачи: