Радиус окружности, описанной около прямоугольного треугольника, равен 15 см, а радиус вписанной в него окружности равен 6см. Найдите длину меньшего катета треугольника.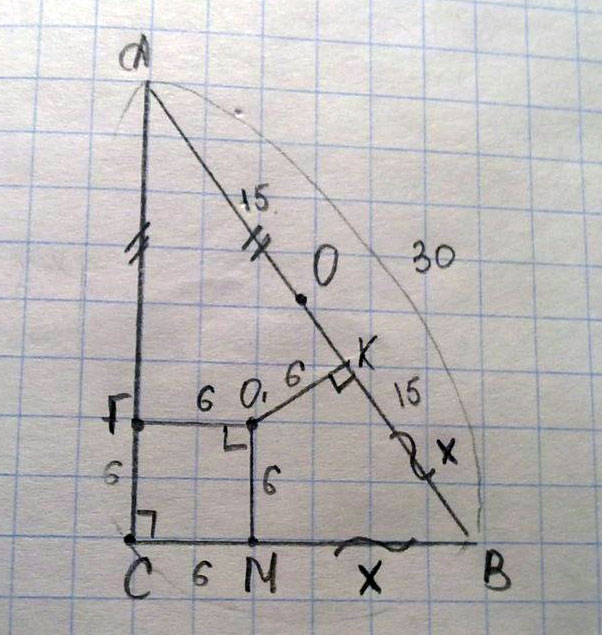

Пусть а и в катеты треугольника, тогда с=30, т.к. радиус описанной окружности равен половине гипотенузы r=p-c,p=r+c=36, P=36*2=72,a+b=72-30=42. имеем{а+в=42  a^2+b^2=900  {a^2+b^2=2*ab=42^2=1764  a^2+b^2=900 {900+2*ab=17642ab=1764-900{a+b=42 ab=432 a^2-42a+432=0   а1=18,а2=24    в1=24, в2=18              Ответ:18