На рисунке AB параллельно CD. a) докажите, что AO:OC= BO:OD. b) Найдите AB, если OD=15см, OB=9см, CD=25см.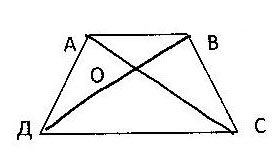

ABCD - трапеция (по определению: АВ || CD, ВС не параллельна AD)


а) Диагонали трапеции разбивают её на 4 треугольника, причём треугольники, прилежащие к основаниям подобны друг другу (по свойству трапеции). Рассмотрим треугольники АВО и CDO: они подобны. Следовательно, АО:ОС=ВО:OD.



б) Так как треугольники АВО и CDO подобны, то АВ:СD=ВО:OD; АВ:25=9:16; АВ=0,5625*25=14,0625 (см)

Ответ: АВ=14,0625 см.



Похожие задачи:
Боковые стороны трапеции равны 12 м и 8 м, большее основание 26 м, а диагональ делит трапецию на два подобных треугольника. Определите длину этой диагонали.



смотреть решение >>
ABCD - Равнобедренная трапеция с основаниями AD и BC, диагонали которой пересекаются в точке О. Докажите, что треугольники AOD и BOC подобны.


смотреть решение >>
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О

а) Сравните площади треугольников ABD и ACD

б) Сравните площади треугольников ABO и CDO

в) Докажите что OA*OB=OC*OD

2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.

3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.


смотреть решение >>
В трапеции ABCD с боковыми сторонами АВ и CD диагонали пересекаются в точке О. а) Сравните площади треугольников ABD и ACD. б) Сравните площади треугольников АВО и СDO. в) Докажите, что выполняется равенство ОА • ОВ = ОС • OD.
смотреть решение >>
Диагональ АС трапеции ABCD делит ее на два подобных треугольника. Докажите, что АС2 =a⋅b, где а и b — основания трапеции.
смотреть решение >>