Дан параллелограмм AXRZ (см. рисунок) Доказать AB биссектриса угла XAZ

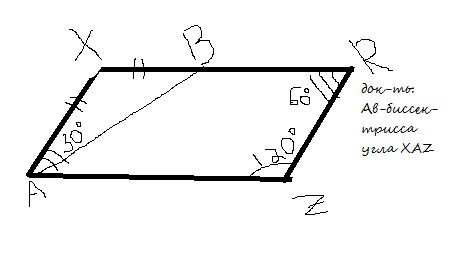
Решение: Рассм. треугольник АХВ - равнобедренный, так как ах=хв по условию. Т.к. угол ХАВ=30градусов => угол ХВА=30градусов => угол АХВ=120 градусов. Т. к. сумма углов, прилежащих к боковой стороне параллелограмма равна 180 градусов => угол ХАZ=60градусов = угол ХАВ + угол ВАZ =>угол ВАZ=угол ХАZ - угол ХАВ=60 градусов - 30 градусов = 30 градусов => угол ХАВ=углу. ВАZ => АВ - биссектриса

в параллелограмме противоположные угла равны, следвательно угол А равен углу Р. Если угол ХАВ раен 30, то угол ВАZ равен 60-30=30. 30=30, по определению биссктрисы, АВ биссектрисса.