Точка М удалена от каждой вершины остроугольного треугольника АВС на 17 см. Вычислить расстояние от т. М до плоскости АВС, если ВС=8 см, угол ВАС=30 градусов.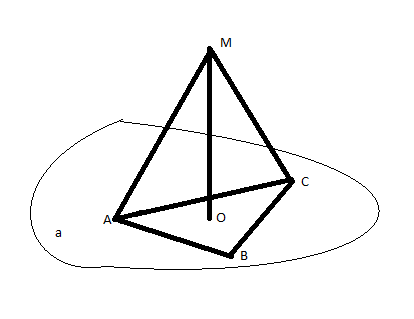

Так как, М равноудалена от вершин, то высота пирамиды МАВС падает в центр описанной окружности АВС. Тогад, по т sin, 8 / sin 30 = 2R, то есть R = 8 = BC. И ВС -- гипотенуза прямоугоьного треугольника. Значит, тогда АВ = корень(256-64) = 24корень из7 и Н = корень( 289-64) = 15. Тогда, объем равен V = 1/3 S *H = 1/3*1/2*8*24корень7*15 = 480корень7