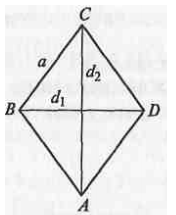
По свойству ромба: BO=OD=3. В треугольнике BOC: $$ CO=OA=\\sqrt{12^2-3^2}=\\sqrt{135} \\ CA=d_1=2\\sqrt{135} \\ P=4*12=48 \\ S=\\frac{1}{2}*d_1*d_2=\\=\\frac{1}{2}*6*2\\sqrt{135}=\\=6\\sqrt{135} $$ Диагонали являются биссектрисами. Угол $$ BCO=DCO=BAO=DAO= \arccos\\frac{1}{4} $$. Угол $$ C=A=\arccos\\frac{1}{2}=60^o $$ Угол $$ OBA=ODA=CBO=CDO= \arcsin\\frac{1}{4} $$. Угол $$ B=D=\arcsin\\frac{1}{2}=30^o $$

Похожие задачи: