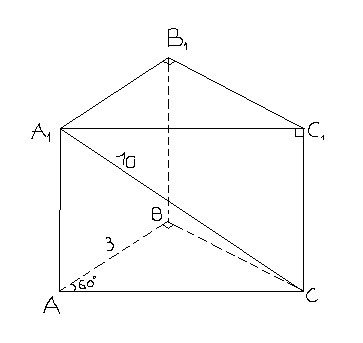
Основание прямой призмы- прямоугольный треугольник с катетом 3 см и прилежащим к

Основание прямой призмы- прямоугольный треугольник с катетом 3 см и прилежащим к нему углом 60 градусов. Диагональ боковой грани, содержащей гипотенузу треугольника, равна 10см. Найдите объем призмы.

Дано:AB=3, угол CAB=60, A1C=10

Решение:угол С=30, значит AC=3*2=6(против угла в 30)

$BC=\sqrt{6^2-3^2}=3\sqrt{3}$

$S_{ABC}=\frac{1}{2}*6*3\sqrt{3}=9\sqrt{3}$ В треугольнику AA1C:

$AA_1=\sqrt{10^2-6^2}=8 \\ V=S_{ABC}*AA_1=9\sqrt{3}*8=72\sqrt{3}\approx124,7$

2. Основание равнобедренного треугольника равно 12 см, а высота, опущенная на основание, - 8 см. Найдите высоту, опущенную на боковую сторону.

3. сторона треугольника, противолежащая углу 60* равна 5 корень из 6 см, а наименьший угол треугольника равен 45*. Найдите наименьшую сторону треугольника.

смотреть решение >>

Найдите объём прямой призмы ABCA1B1C1, если угол BAC=120 градусов, AB=5, AC=3, а наибольшая из площадей боковых граней равна 35 кв. см

смотреть решение >>

Oснованием прямой призмы служит треугольник со сторонами 10, 10 и 12. Через большую сторону нижнего основания и середину противоположного бокового ребра проведена плоскость под углом 60 к плоскости основания. Найдите обьем призмы. пожайлуста.
смотреть решение >>

В прямой призме ABCA1B1C1 угол С=90 градусов, АС = 6 см, угол ВАС = 45 градусов, объем призмы равен 108кубических см, найти площадь полной повернхность призмы?

смотреть решение >>

В равнобедренном треугольнике ABC AB=AC, AB=6,

$cosB =\frac{\sqrt3}{2}$ Найдите его площадь.
смотреть решение >>