Медиана AM треугольника ABC равна отрезку ВМ. Докажите, что один из углов треугольника ABC равен сумме двух других углов.
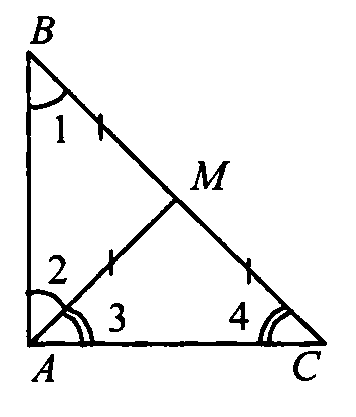
ΔАВМ- равнобедренный, потому что ВМ= МА, тогда ∠1 = ∠2.
ΔАМС - равнобедренный, потому что АМ= МС, тогда ∠3 = ∠4.
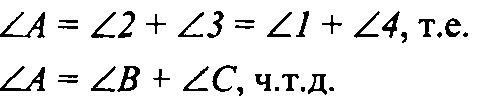
Похожие задачи: