Найти площадь равнобокой трапеции 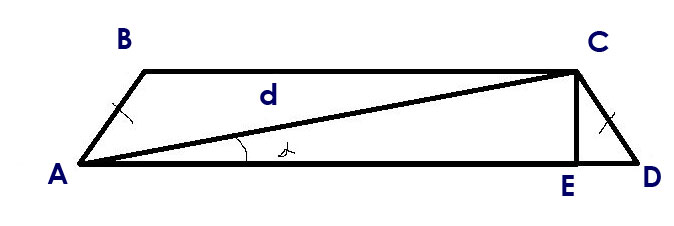
Площадь трапеции:S = (a+b)*h/2 (1) В нашей трапеции: а = AD, b = BC, h = CE
Выразим через основания трапеции отрезок АЕ:АЕ = AD - DE = a - (a-b)/2 = (a+b)/2.
Теперь рассмотрим пр. тр-ик АСЕ:СЕ = h = d*sina.
(2)AE = (a+b)/2 = d*cosa.
(3) Подставим (2) и (3) в (1):$$ S=d^2*sina*cosa, $$
Или по формуле синуса двойного угла:
$$ S = \frac{1}{2}d^2*sin2a. $$
Выразим через основания трапеции отрезок АЕ:АЕ = AD - DE = a - (a-b)/2 = (a+b)/2.
Теперь рассмотрим пр. тр-ик АСЕ:СЕ = h = d*sina.
(2)AE = (a+b)/2 = d*cosa.
(3) Подставим (2) и (3) в (1):$$ S=d^2*sina*cosa, $$
Или по формуле синуса двойного угла:
$$ S = \frac{1}{2}d^2*sin2a. $$
Похожие задачи: