Докажите, что биссектрисы острых углов прямоугольного треугольника при пересечении образуют угол 45 градусов.

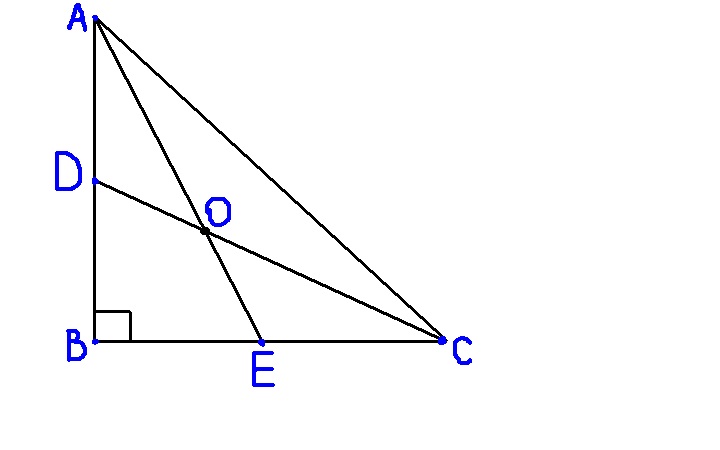
Дано: треуг АВС, Угос В=90 гр, АЕ,CD -биссектрисы. Доказать: угол DOA=уг ЕОС = 45 гр. Д-во.1) Пусть уг DOA=х, тогда уг САЕ=х, т.к. АЕ биссектриса. Сумма углов треуг = 180 гр, следовательно уг АСВ=180-90-2х=90-2хCD -биссектриса угла АСВ, значит уг DСА=(90-2х):2=45-х2) Рассмотрим треугольник ВАЕ, угол АЕВ=180-90-х=90-х3) АЕВ и АЕC смежные, в семме 180, АЕС=180-(90-х)=90+х4) Из треугольника ЕОС: угол ЕОС=180-(90+х)-(45-х)=455) ЕОС и АОD вертикальные, значит равны. 

---

Вариант 2


Дан прямоугольный треугольный треугольник, угол В прямой (равен 90 градусов). Сумма острых углов прямоугольного треугольника равна 90 градусовт.е. угол САВ+угол. ВСА=90 градусов. АЕ и CD -биссектриссы острых углов. По определению биссектрисы делят угол пополам, поэтомуугол CAE=угол BAE=1/2 *угол ВАСугол ACD=угол BCD=1/2*угол *ВСА остюда угол CAE+угол ACD=1/2 *угол ВАС+1/2*угол *ВСА==1/2*(угол САВ+угол. ВСА)=1/2*90 градусов=45 градусов Сумма углов треугольника равна 180 градусов, поєтомуугол AOC=180-угол-CAE - угол ACD=180-(угол CAE+угол ACD)=180-45=135 градусов. Сумма смежных углов равна 180 градусов, поэтомуугол AOD=180-135=45 градусов - это один из углов образуемых при пересечении биссектрис острых данного прямоугольного треугольника,таким образом мы доказали требуемое утверждение. Доказано