Доказать, что треугольник KPX равен треугольнику XYK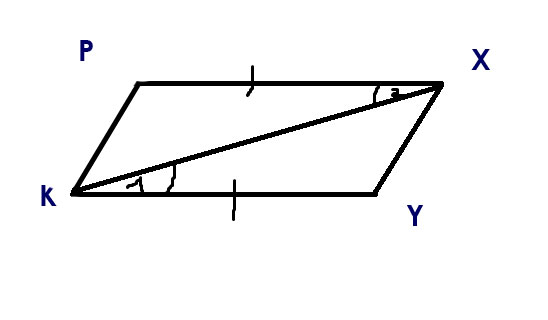

треугольник KPX= треугольнику КХУ ( по 1 признаку), т.к. сторона КХ-общая, РК=КУ(по условию) и угол РХК= углу XKY (по условию).



Дано:KPXY-параллKX-диагональPX=KYуголPXK=уголYKXДоказать:треугKPX=треугXYKДоказательство:Т.к. PX=KY(по усл), уголPXK=уголYKX(по усл), KX-общ. сторона, из этого следует что треугKPX=треугXYK(по первому признаку рввенства треуг, то есть по двум сторонам и углу между ними) что и требовалось доказать






Похожие задачи:
В равнобедренном треугольнике PXE, D- середина основания PE. DA и DB- перпендикуляры к боковым сторонам. Доказать: угол ADX=углу XDB


смотреть решение >>
На биссектрисе угла А взята точка В, а на сторонах угла - точки C и D, такие, что угол АВС = углу АВD. Доказать что AD=AC.
смотреть решение >>
Периметр параллелограма АBCD равен 12см, а периметр треугольника ABD-8см. Найти длину диаганали BD

Какую фигуру можно построить, последовательно соединяя середины сторон 1)параллелограма; 2)прямоугольника; 3) ромба; 4) квадрата. Обоснуйте ответ

Отрезки АВ и СD пересекаются в точке О,которая является серединой кажодго из этих отрезков. Верно ли равенство треуг. АОС=треуг. ВОD? Укажите при каких условиях эти задачи другие пары равных треугольников.


смотреть решение >>
Вставьте на место пропусков.

Задание:

На рисунке точка М делит сторону АС треугольника АВС в отношении АМ:МС=2:3. Площадь треугольника АВС равна 180 см квадратных. Найдите площадь треугольника АВМ.

Решение:

Треугольники АВМ и АВС имеют общую высоту ВD, поэтому их площади относятся как основания______и ____. Так как по условию АМ:МС=2:3, то АМ:АС=____:____ и S треугольника АВМ : S треугольника АВС =____:____, откуда S треугольника АВМ=____S треугольника АВС=____*180 см квадратных=____см квадратных

Ответ:____см квадратных.


смотреть решение >>
Каким условиям должны удовлетворять два равносторонних треугольника чтобы один из них можно было получить из другого при помощи параллельного переноса?
смотреть решение >>