1. Площадь ромба $$ S=54\sqrt3 $$за формулой $$ S=a^2sin\alpha, $$ где \(\alpha\) - острый угол между сторонами ромба, найдем его сторону: $$ 54\sqrt3=a^2sin60 \\ a^2=\frac{54\sqrt3}{sin60} \\ a^2=\frac{54\sqrt3}{\frac{\sqrt3}{2}}=\\={54\sqrt3}\cdot\frac{2}{\sqrt3}=54*2=108 \\ a=\sqrt{108}=4\sqrt7 $$


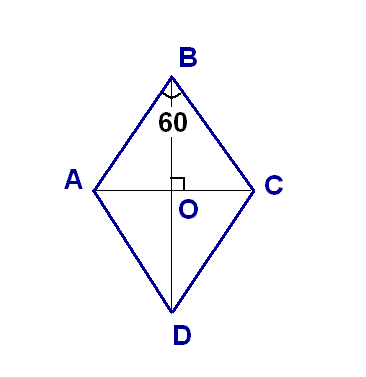
2. Диагонали ромба пересекаются под прямым углом, значит угол АОВ = 90 градусов. диагонали ромба также являются его биссектрисами. т.о. угол АВО=30. значит треугольник АОВ - прямоугольный (угол АОВ=90) с острым углом АВО = 30.и что следует с п.1 стороной $$ а= 4\sqrt7 $$.


3. $$ cosABO=\frac{BO}{AB} \\ BO=AB\cdot cos{ABO} \\ BO=4\sqrt{7} \cdot cos30 = 4\sqrt{7} \cdot \frac{\sqrt3}{2}=2 \cdot \sqrt{21} \\ BD=2*BO BD=2* \\BD=2 \cdot BO= 2 \cdot 2 \sqrt{21} = 4 \sqrt{21} $$

Похожие задачи: