Дано: ABCD - параллелограмм; АВ = а; ВС = b; Угол A = a. Найти: АС = ?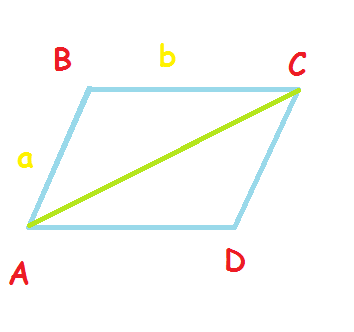

Решение: По Т. Косинусов, AC² = a² + b² - 2abcos(90° - α) = a² + b² - 2absinα ⇒ AC = √(a²+ b² - 2absinα). В ответах AC = √(a² + b² + 2abcosα).

УголA = a; УголВ =180-a; А вот теперь по Т. Косинусов, AC² = AB² + BC² - 2*AB*BC*cos B AC² = a² + b² - 2abcos(180° - α) = a² + b² - 2ab *(-cos α)=a² + b² + 2absinα; AC = √(a² + b² + 2abcosα)