Проиллюстрируйте с помощью кругов Эйлера соотношение между множеством N натуральных чисел, множеством Z целых чисел, множеством Q рациональных чисел. Найдите пересечение и объединение:
а) множества натуральных и множества целых чисел;
б) множества целых и множества рациональных чисел;
в) множества рациональных и множества иррациональных чисел.
Решение: 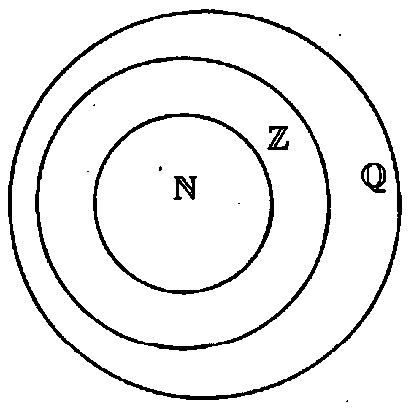
а) N ∩ Z = N; N U Z = Z;
б) Z ∩ Q = Z; Z U Q = Z;
в) N ∩ I = 0; N U I = R.
Похожие задачи:
Проиллюстрируйте с помощью кругов Эйлера соотношение между множествами - А и В и найдите пересечение и объединение этих множеств, если:
а) А - множество целых чисел, кратных З, В - множество целых чисел, кратных 5;
б) А - множество целых чисел, кратных З, В - множество целых чисел, кратных 15.
1) Распределите, кто выполняет задания для случая а), а кто - для случая б), и выполните их.
2) Проверьте друг у друга, верно ли выполнен рисунок и правильно ли найдены пересечение и объединение множеств А и В.
3) Исправьте ошибки, если они допущены.смотреть решение >> Известно, что X - множество простых чисел, не превосходящих 20, а У - множество двузначных чисел, не превосходящих 20. Задайте множества X и У перечислением элементов и найдите их пересечение и объединение.
Ответ:
X = {2,3,5,7,11,13,17,19}.
Y = {10,11,12,13,14,15,16,17,18,19,20}.
XUY = {2,3,5,7,10,11,12,13,14,15,16,17,18,19,20}
X∩Y = {11,13,17,19}.смотреть решение >>