Докажите, что при любом натуральном n значение выражения

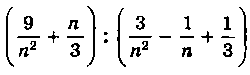
является натуральным числом.

(Задача-исследование.) Верно ли, что при любом натуральном n значение выражения
√n(n + 1)(n + 2)(n + 3) + 1 является натуральным числом?
1) Выберите произвольное значение n и проверьте, является ли натуральным числом соответствующее значение корня.
2) Подумайте, как удобно сгруппировать множители в произведении n(n + 1)(n + 2)(n + 3), чтобы представить подкоренное выражение в виде квадрата.
3) Выполните преобразования и дайте ответ на вопрос задачи.
смотреть решение >>

Докажите, что при любом натуральном n значение дроби является натуральным числом:
     10n-1
а) --------;
        9
    10n+8
б) --------;
       9
     10n-4
в) --------.
       3
смотреть решение >>

Докажите, что:
а) при любом натуральном значении n значение выражения n(n + 5) - (n - 3)(n + 2) кратно 6;
б) при любом натуральном значении n, большем 2, значение выражения (n - 1)(n + 1) - (n - 7)(n - 5) кратно 12.
смотреть решение >>

а) Докажите, что при любом натуральном п значение выражения (4n + 5)² - 9 делится на 4.
б) Докажите, что при любом натуральном п значение выражения (n + 7)² - n² делится на 7.
смотреть решение >>

Докажите, что при любом целом а и дробном х значение выражения

является четным числом.
смотреть решение >>